Selasa, 28 Juli 2020

Matematika Kelas 7 (bcdef) BAB 1 BILANGAN BULAT

Kenalan dulu ya sebelumnya :)



Bilangan Bulat

Bilangan bulat adalah bilangan yang terdiri dari tiga jenis bilangan, yaitu

bilangan negatif, nol, dan bilangan positif.


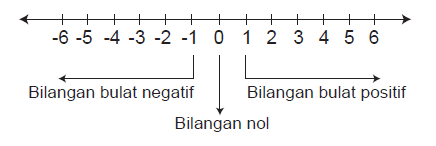
Ketiga jenis bilangan ini bisa dilihat pada garis bilangan yang dibuat, dengan bilangan nol berada di tengah, kemudian di sisi kiri nol ada bilangan negatif, dan di sisi kanan nol adalah bilangan positif.

Nol bukanlah bilangan positif maupun negatif, teman-teman, karena nol adalah bilangan tersendiri.

Kesimpulannya, bilangan bulat terdiri dari bilangan bulat positif, seperti 1, 2, 3, lalu ada bilangan nol, dan terdiri dari bilangan bulat negatif, seperti -1, -2, -3, dan seterusnya.


Operasi Hitung

Dalam operasi hitung, ada beberapa operasi, dimulai dari penjumlahan dan pengurangan.

Penjumlahan adalah operasi hitung yang dilambangakn dengan tanda tambah atau +, dan pengurangan dilambangkan dengan tanda kurang atau -.

Contohnya adalah operasi hitung 5 + 3 = 8 untuk penjumlahan dan 5 - 4 = 1 untuk pengurangan.

Nah, dua operasi hitung ini dapat diselesaikan dengan menggunakan garis bilangan dengan menambah atau mengurangi bilangan pertama dengan bilangan kedua.


Operasi hitung yang berikutnya adalah perkalian dan pembagian.

Contoh Soal Perkalian:

(+) x (+) = +      contoh: 2 x 5 = 10

(+) x (-) = –        contoh: 3 x (-1) = -3

(-) x (+) = –        contoh: (-9) x 2 = -16

(-) x (-) = +        contoh: (-2) x (-7) = 14

Contoh Soal Pembagian:

(+) : (+) = +      contoh: 20 : 2 = 10

(+) : (-) = –        contoh: 30 : (-5) = -6

(-) : (+) = –        contoh: (-10) : 5 = -2

(-) : (-) = +        contoh: (-4) : (-1) = 4

Sifat yang pertama dari operasi hitung keduanya adalah bahwa positif dikali positif, maupun negatif dikali negatif hasilnya adalah positif.

Bilangan negatif dibagi dengan negatif dan negatif dikali bilangan negatif juga akan menghasilkan bilangan positif.

Sifat yang ketiga adalah bilangan positif dikali negatif sama dengan negatif, begitu juga pada pembagian.

Sifat terakhir adalah bilangan negatif dikali bilangan positif hasilnya negatif, dan bilangan negatif dibagi bilangan positif, hasilnya negatif.

Dari keempat sifat itu, diketahui bahwa dua bilangan bertanda sama, maka hasilnya adalah bilangan positif. Sedangkan bilangan dengan tanda berbeda akan menghasilkan bilangan negatif.


Hitung Campur

Sesuai namanya, pada operasi hitung ini mencampurkan beberapa operasi hitung, seperti penjumlahan, pengurangan, perkalian, hingga pembagian.

Dalam operasi hitung dampur ini ada tangga kelas, yang terdiri dari tanda kurung di paling atas, tanda bagi dan kali di bawhanya, lalu ada tanda negatif dan positif di tangga paling bawah.

Urutan simbol pada hitung campur ini menunjukkan cara atau urutan pengerjaan operasi itu, teman-teman.

Artinya, setiap satu tangga maka kita mengerjakan dari kiri. Maka kalau dalam sebuah soal ada berbagai tanda tadi, kita harus mengerjakannya dari tanda kurung lebih dulu, sesuai dengan urutan pada tangga kelas.


KPK dan FPB

Untuk mengetahui mengenai KPK dan FPB, kita harus tahu lebih dulu mengenai bilangan prima, yaitu bilangan yang hanya punya dua faktor, yaitu bilangan satu, dan bilangan itu sendiri.

Contohnya bilangan 2, 3, 5, 7, 11, dan seterusnya. Bilangan prima inilah yang nantinya akan digunakan pada pohon faktor dalam operasi KPK dan FPB.

Nah, KPK sendiri adalah singkatan dari kelipatan persekutuan terkecil, yaitu hasil kali faktor prima yang berbeda dengan mengambil pangkat tertinggi.

Sedangkan FPB adalah faktor persekutuan terbesar, yaitu hasil kali faktor-faktor prima yang sama dengan mengambil pangkat terendah.

Untuk mencari hasil dari KPK dan FPB, menggunakan cara yang sama, yaitu menggunakan pohon faktor.

Soal dan Pembahasan

1. Perhatikan perubahan suhu berikut ini:

a. Suhu udara di Kota Tokyo pagi hari -4 derajat Celcius, pada siang hari suhu itu naik 12 derajat Celcius, dan pada malam hari suhu turun 9 derajat Celcius dari siang hari.

b. Suhu di Kota London pagi hari -5 derajat Celcius, pada siang hari suhu itu naik 13 derajat Celcius, dan pada malam harisuhu turun 8 derajat Celcius dari siang hari.

c. Suhu udara di Kota Amsterdam pagi hari -6 derajat Celcius, pada siah hari suhu itu naik 19 derajat Celcius dan pada malam hari suhu turun 11 derajat Celcius dari siang hari.

Menurut Anton, kota dengan suhu paling dingin pada malam hari adalah Kota Tokyo. Apakah pendapat Anton benar? Jelaskan alasanmu!


Pendapat Anton benar, karena udara di Kota Tokya pada malam hari lebih dingin dibandingkan kota lainnya.

Suhu Kota Tokyo: -4 +12 = 8 - 9 - -1 derajat Celcius

Suhu Kota London: -5 +13 = 8 - 8 = 0 derajat Celcius

Suhu Kota Amsterdam: -6 + 19 = 13 - 11 = 2 derajat Celcius


2. Dalam suatu ujian matematika diberlakukan aturan, apabila jawaban benar mendapatkan skor 4, apabila salah skornya -2, dan tidak menjawab skornya 1. Dari 40 soal yang diberikan, Budi menjawab 22 soal dengan benar dan 10 soal salah. Menurut Budi, ia akan mendapat skor 68. Apakah pendapat Budi benar? Jelaskan pendapatmu!

Soal yang dapat dijawab dengan benar oleh Budi: 22 x 4 = 88

Soal yang dijawab dengan salah oleh Budi: 10 x -2 = -20

Soal yang tidak djiawab Budi: 8 x 1 = 8

Sehingga nilainya, 88 -20 + 8 = 76. Jadi skor yang bisa didapatkan oleh Budi adalah 76.


3. Aldi berenang setiap tiga hari sekali. Beni berenang di tempat yang sama setiap lima hari sekali, sedangkan Erwin berenang seminggu sekali. Pada tanggal 30 April, mereka bertiga berenang bersama-sama. Aldi mengatakan mereka akan berenang bersama lagi pada tanggal 13 Agustus. Benarkah perkataan Aldi tersebut? Jelaskan alasanmu!

Dari pernyataan Aldi, maka benar ketiganya akan berenang bersama lagi di tanggal 13 Agustus.

Jawaban ini didapatkan dengan mencari KPK dari 3, 5, dan 7, yang hasilnya adalah 105.

Sedangkan 105 hari dari tanggal mereka berenang bersama, yaitu 30 April adalah 13 Agustus.


Klik dibawah ini ya buat latihan!!!

LATIHAN SOAL BILANGAN BULAT

Diposting oleh di Tidak ada komentar:

Selasa, 17 Maret 2020

INI UNTUK SEMESTER 2 YAA

BAB 5 

PENYAJIAN DATA

Mengenal Data

Data merupakan kumpulan keterangan atau informasi yang diperoleh dari hasil pengamatan suatu objek dan disajikan secara jelas.
Cara memperoleh data :
1. Wawancara adalah data yang diperoleh dengan cara menanyakan langsung kepada      
    narasumber.
2. Angket adalah data yang diperoleh dengan mengkajikan variasi pernyataan yang 
    mendukung topik yang diteliti.
3. Observasi adalah cara yang diperoleh melalui pengamatan langsung terhadap objek 
    yang sedang diteliti.

Penyajian Data: Diagram Lingkaran, Batang, Garis


Penyajian data dapat dilakukan dengan cara menyajikan data dalam bentuk diagaram. Diagram tersebut dapat berupa lingkaran, batang, atau garis. Tujuan dari penyajian data adalah untuk mempermudah pembaca dalam melihat data.
CONTOH

Daftar Berat Badan 60 siswa SMP N 1 Sukaraja:
43, 40, 42, 42, 43, 44, 41, 44, 43, 42, 42, 43,
41, 40, 40, 44, 41, 40, 42, 42, 44, 43, 40, 40,
43, 44, 44, 41, 41, 41, 41, 42, 43, 44, 43, 43,
41, 43, 41, 42, 43, 41, 43, 42, 43, 41, 43, 44,
41, 43, 42, 42, 42, 42, 44, 43, 42, 42, 43, 43.
Data di atas akan kita sajikan dalam bentuk diagram lingkaran, batang, dan garis. Sebelumynya, untuk mempermudah prosesnya, kita buat data di atas ke dalam tabel distribusi frekuensi seperti terlihat pada tabel di bawah.
Tabel Distribusi Frekuensi

 penyajian data dalam tabel
Dengan menggunakan tabel frekuensi di atas, kita akan membuat penyajian data dalam bentuk diagram lingkaran, batang, dan garis. Penyajian data pertama yang akan dibahasa adalah diagram lingkaran.

Diagram Lingkaran

Penyajian dalam bentuk lingkaran dibedakan menjadi dua, yaitu dalam bentuk derajat dan persen. Untuk menyajikan data dalam bentuk lingkaran dalam bentuk derajat, kalian perlu merubah banyak data sesuai perbandingan dalam derajat. Begitu juga untuk penyajian data bentu diagram lingkaran dalam persen. Kalian perlu merubah banyak data ke dalam persen.
Perhatikan proses penyajian data dalam bentuk lingkaran dalam derajat dan persen yang akan dibahas di bawah.

Diagram Lingkaran dalam Derajat (^{o})

Perhitungan banyaknya data ke dalam derajat:
  \[ \textrm{Berat 40 kg} = \frac{6}{60} \times 360 = 36^{o} \]
  \[ \textrm{Berat 41 kg} = \frac{12}{60} \times 360 = 72^{o} \]
  \[ \textrm{Berat 42 kg} = \frac{15}{60} \times 360 = 90^{o} \]
  \[ \textrm{Berat 43 kg} = \frac{18}{60} \times 360 = 108^{o} \]
  \[ \textrm{Berat 44 kg} = \frac{9}{60} \times 360 = 54^{o} \]
Setelah mendapatkan data dalam bentuk derajat seperti data di atas, buatlah diagarm lingkaran yang sesuai seperti terlihat pada gambar di bawah.

Diagram Lingkaran dalam Persen (%)
diagram lingkaran dalam derajat
Perhitungan banyaknya data ke dalam persen:
  \[ \textrm{Berat 40 kg} = \frac{6}{60} \times 100 \% = 10 \% \]
  \[ \textrm{Berat 41 kg} = \frac{12}{60} \times 100 \% = 20 \% \]
  \[ \textrm{Berat 42 kg} = \frac{15}{60} \times 100 \% = 25 \% \]
  \[ \textrm{Berat 43 kg} = \frac{18}{60} \times 100 \% = 30 \% \]
  \[ \textrm{Berat 44 kg} = \frac{9}{60} \times 100 \% = 15 \% \]

Setelah mendapatkan data dalam bentuk derajat seperti data di atas, buatlah diagarm lingkaran yang sesuai seperti terlihat pada gambar di bawah.
diagram lingkaran dalam persen


Diagram Batang

Penyajian data ke dalam bentuk diagram batang cukup mudah dilakukan dibanding diagaram lingkaran. Kalian hanya perlu menyesuaikan keterangan data dan banyak data pada masing-masing sumbu x dan y. Selanjutnya, kalian hanya perlu menggambar batangnya sesuai data yang diketahui.
Penyajian data dalam bentuk diagram batang dapat dilihat pada gambar di bawah.
penyajian data dalam diagram

Diagram Garis

Cara menyajikan data dalam bentuk diagram garis hampir sama dengan diagram batang. Bedanya terletak pada langkah akhirnya. Pada diagram batang hasil akhirnya adalah menggambar batangnya. Pada diagram garis, kalian hanya perlu menarik garis dari titik-titik yang telah disesuaikan dengan data yang diketahui.
Hasil penyajian data dalam bentuk diagram garis dapat dilihat pada gambar di bawah.

 penyajian data dalam bentuk diagram garis

Contoh Soal dan Pembahasan

Contoh 1
Diagram lingkaran berikut menunjukkan kegemaran 300 siswa dalam mengikuti kegiatan ekstrakurikuler di suatu sekolah.

 statistika: penyajian data, mean, median, dan modus

 Banyak siswa yang mengikuti kegiatan ekstrakurikuler drama adalah ….
A.     30 orang
B.     35 orang
C.     40 orang
D.     45 orang

 Pembahasan:
Persentase siswa yang mengikuti kegiatan ekstrakurikuler drama adalah
  \[\% Siswa \; ekskul \; drama = 100 \% - (12 \% + 20 \% +30 \% +10 \% + 13 \%) \]
                                            \[ = 100 \% - 85 \% \] \[ = 15 \% \]

Banyak siswa yang mengikuti kegiatan ekstrakurikuler drama adalah
  \[ = 15 \% \times \textrm{total siswa} \]
  \[ = 15 \% \times 300 \]
  \[ = \frac{15}{100} \times 300 \]
  \[ = 45 \; \textrm{siswa} \]

 Jadi, banyak siswa yang mengikuti kegiatan ekstrakurikuler drama adalah 45 orang.
Jawaban: D

 Contoh Soal Penyajian Data 2 (SOAL UN Matematika SMP 2016)
“Pengunjung Perpustakaan”
Suatu hari Ani menemukan sobekan koran yang memuat data pengunjung perpustakaan berupa gambar diagram batang sebagai berikut.

 Statistika: Penyajian Data, Mean, Median, dan Modus
Rata-rata Pengunjung 41 Orang Selama Lima Hari.
Informasi yang ada pada koran tersebut menunjukkan data pengunjung perpustakaan selama 5 hari. Ani penasaran ingin tahu tentang banyak pengunjung pada hari Rabu. Tolong bantu Ani, berapa banyak pengunjung pada hari Rabu?
A.     55 orang
B.     60 orang
C.     65 orang
D.     70 orang

Pembahasan:
Banyak pengunjung:
Senin = 45 orang
Selasa = 40 orang
Rabu = x orang
Kamis = 30 orang
Jumat = 20 orang

 Rata-rata pengunjung 41 orang selama lima hari.
  \[ Rata-rata = \frac{45 + 40 + x + 30 + 20}{5} \]
  \[ 41 = \frac{135 + x}{5} \]
  \[ 41 \times 5 = 135 + x \]
  \[ 205 = 135 + x \]
  \[ x = 205 - 135 = 70 \]

 Jadi, banyak pengunjung pada hari Rabu adalah 70 orang. Jawaban: D


TUGAS INDIVIDU MATEMATIKA


ULANGAN HARIAN MATEMATIKA


                                                        GURU MAPEL
RISTIN RAHMAWATI, S.Pd
Diposting oleh di Tidak ada komentar:
Langganan: Postingan (Atom)